Q: When I plot a terrain profile the Fresnel zone sometimes appears to be non-symmetrical. Is this an error?

A: The line of sight (LOS) from the transmitter antenna center of radiation to the receiver antenna center of radiation and the Fresnel zone for the path at a given frequency can be added to a profile plot. The plot can be drawn to show the effects of earth curvature either by "bending" the terrain upward or by bending the LOS and Fresnel zone downward. First, consider the simpler case of bending the terrain upward and not adjusting the LOS or Fresnel plot.

When the earth curvature is shown by adjusting the terrain elevation values upward, the line of sight is simply a straight line between the two end points. The Fresnel zone is computed along the path, usually for the distance of each of the terrain points, so the resolution of the computed and plotted Fresnel zone is comparable to the terrain data. The N^th Fresnel zone formula is a function of the wavelength (l ) and the distance along the path from each endpoint (D₁ and D₂):

This value represents a perpendicular distance from the direct line of sight line. The combination of these points along the path can be viewed as the Fresnel zone plot. Typically the first Fresnel zone (N=1) is used to determine obstruction loss, with methods such as Bullington. Anytime the path clearance between the terrain and the line of sight path is less than 0.5F₁ (half of the first Fresnel zone distance), some knife edge diffraction loss will occur.

Clearly from the formula, the Fresnel zone is symmetrical, with a value of zero at each end (where either D₁ or D₂ is zero) and a maximum at the center of the path. However, often the plot of the Fresnel zone will appear distorted, or non-symmetrical, especially on steep paths, i.e., paths with a large difference between the end point elevations.

The reason for this unusual appearance is the geometry of the plot, and the exaggerated aspect ratio. For example, a profile plot may represent a horizontal scale of 25-miles, and a vertical scale of 1000 feet. The scale shown on the page is necessarily distorted in order to show both 1000 feet and 25 miles (or 132000 feet). When plotting the Fresnel zone in the context of this distorted aspect ratio, it would be incorrect to simply measure the Fresnel zone distance out perpendicular from the line of sight path. For example, suppose at a point along the path the computed Fresnel zone distance is 20 feet. Plotting a point 20 feet from the LOS would seem to be as simple as the drawing shown below:

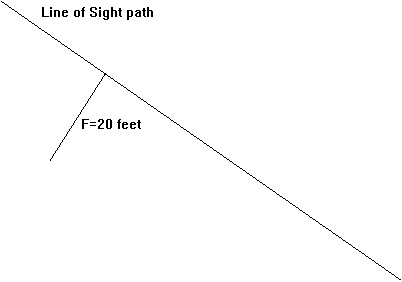
However, plotting the Fresnel zone point at a distance of 20 feet from the line of sight can be viewed as shown below. For example, if the angle of the line of sight is 35° the vertical and horizontal distances are as shown:

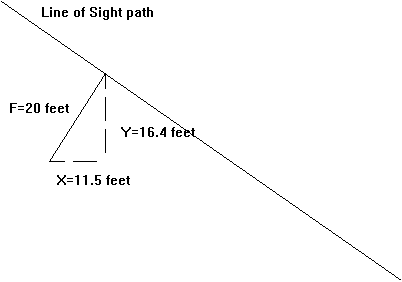
On the profile plot with a non-unity aspect ratio, this means that the vertical difference from the point on the line of sight to the corresponding Fresnel zone point is 16.4 feet, and the horizontal difference is 11.5 feet. But the horizontal displacement must be plotted consistent with horizontal scale of the profile plot, which is in miles. Therefore, the horizontal displacement must be considered as .002 miles. The actual location of the Fresnel zone point on a typical profile plot might look more like the following drawing:

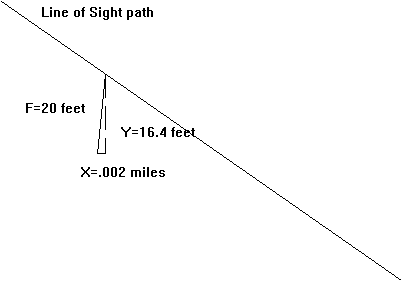
As you can see, when the Fresnel zone point is drawn with the scaling of the drawing in mind, the point will appear shifted toward the end of the path on this "downhill" path. The opposite shift would be observed on a path that is "uphill", and the effect is minimized for a path that is almost level. When you compute all of the Fresnel zone points along the path, including this shift for scaling, and then connect the points to draw the Fresnel zone, the result will appear to be non-symmetrical. For a near-level path, the shift is less and the Fresnel zone will appear more symmetrical. The Fresnel zone is computed as a new set of X and Y values and is then plotted on the profile. Note that the array of X values for the Fresnel zone will not be the same as the array of values for the terrain data or the LOS path, since the Fresnel zone X values are shifted as described above.

It is also possible to show the earth curvature correction by bending the LOS and Fresnel zone plots downward. In this case, the terrain values are plotted without any upward correction. The result is the same in the sense that the plot shows the relative position of the terrain, LOS, and Fresnel zone, including the effects of atmospheric diffraction. Hence the relative clearance or blockage between the terrain and LOS/Fresnel zone should appear the same whether we are bending the terrain up or the LOS down.

The advantage of showing the atmospheric diffraction by bending the LOS down is that multiple effective earth curvature values can be shown on a single plot. The effect of atmospheric diffraction is to make it appear as if the radius of the earth is larger or smaller, changing path parameters such as clearances, horizons, etc. Showing the bending effect by distorting the LOS down means that the plot of the terrain itself is not affected by the bending, and multiple LOS paths can be drawn, showing different curvature values, so the clearance between the terrain and the LOS/Fresnel can be observed for different values.

When the LOS is plotted to show the effective earth curvature, an array of points is computed for the elevations along the LOS. This is accomplished with simple trigonometry, using the difference in elevation between the end points. Typically the elevations are computed at the same distances used for the terrain path distance array. Then this array of elevation values for the LOS is used to generate another array of adjusted values. The path distance array and this adjusted elevation array are used as the X and Y values for plotting the LOS, which will now appear as a line bent downward, since the elevation of each point on the LOS is moved straight down to indicate the effective elevation of the LOS at that path distance.

To show the Fresnel zone including effective earth curvature, the Fresnel zone X and Y arrays are computed exactly as described above. Then these two arrays (of elevation and distance) are used to generate a new Fresnel elevation array, which contains adjusted Fresnel elevations to indicate the effective Fresnel elevation at that distance (in the Fresnel distance array, not the path distance array). The Fresnel distance array and the adjusted Fresnel elevation array are used as the X and Y values for plotting the Fresnel zone, which will now appear to be bent downward even more than the Fresnel value, since the elevation of each point on the Fresnel zone is moved straight down to indicate the effective elevation that Fresnel distance.

  Search SoftWright Website